Remember yourself calculating electric field intensity, current density or vector potential in idealised cases during your 12th standard. Those problems really gave a summary of the electromagnetics (EM) working in different situations. Advancing further you may recall having calculated the field quantities in case of dipole antennae (standard case). Well these problems were easy to analyse because of the symmetry existing in those situations: Just apply the Maxwell equations and symmetry will do its work.
But what if the problem’s geometry is not symmetric, what if there is an urgent need to find the parameters without going much into the mathematics, what if a practical situation (for example, studying effects of mobile phone on pacemaker) needs to be analysed in a couple of hours?
Surely calculating each Maxwell equation and approximating them will not be a fast solution to the situation from industry point of view. In these situations we use electromagnetic modelling or, precisely, computational electromagnetics.
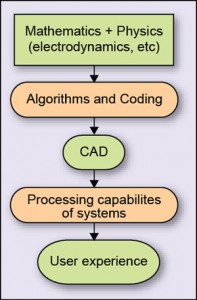
Computational electromagnetics (CEM) is a very challenging and multidisciplinary science that aims at finding solutions of Maxwell equations at boundary conditions (broadly the material boundaries of geometry). It involves numerical methods, efficient (not effective) algorithms and their computer implementations (see Fig. 1).
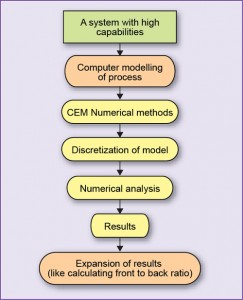
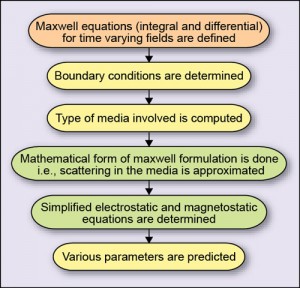
The CEM implementation should have following characteristics:
Accuracy. The results should be accurate to the real situations.
Stability. Results should be stable, which means, if the parameters and excitation are changed then its output should be predictable, that is, it should not become unstable.










