 Audio frequencies range from 20Hz to 20kHz but these frequencies are not heard in the same way. Frequencies below 20Hz and above 20kHz are very difficult to hear, while those not much more than 20Hz, or not much less than 20kHz, cannot be heard by most people. We often need to process these audio signals for various applications. MATLAB is one of the best signal analysis and signal processing tools.
Audio frequencies range from 20Hz to 20kHz but these frequencies are not heard in the same way. Frequencies below 20Hz and above 20kHz are very difficult to hear, while those not much more than 20Hz, or not much less than 20kHz, cannot be heard by most people. We often need to process these audio signals for various applications. MATLAB is one of the best signal analysis and signal processing tools.
Audio compression is a very good example of speech and signal processing. We use the Internet for various purposes including entertainment. Audio is common in all entertainment applications. If an audio file size is large, it takes more space to store.
Audio/video compression frees up space substantially, which can then be utilised for other purposes. This article describes some important audio compression techniques.
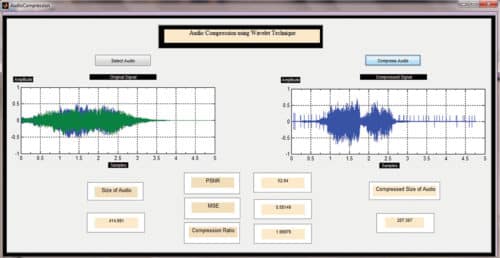
An audio signal sample is taken and analysed using MATLAB for frequency and amplitude. Haar and Daubenches algorithms are applied on the speech signal and the audio is compressed. Audio sizes before and after compression are compared.
The following parameters are compared by the program: Peak signal-to-noise ratio (PSNR), normalised root-mean-square error (NRMSE) and compression ratios.
Haar wavelet algorithm performs the following functions:
1. Selects audio and finds actual signal size
2. Finds amplitude and frequency
3. Creates frame
4. Decomposes the signal spectrum into wavelet
5. Creates psychoacoustic model
6. Inspects the spectrum and finds tones maskers
7. Applies mu-law of compression
8. Finds and corrects offset
9. Rewrites wave
10. Finds the size of compressed signal
Daubenches wavelet transform performs the following functions:
1. Selects audio and finds the actual signal size
2. Finds amplitude and frequency
3. Chooses a block size
4. Changes compression percentages
5. Initialises compressed matrix
6. Does compression using inverse discrete cosine transform (IDCT)
7. Rewrites signal
8. Finds the size of compressed signal
For complete algorithms, refer code implementations.
MATLAB code file AudioCompression.m implements Haar wavelet and AudioCompression2.m file implements Daubenches wavelet. In this example, Windows XP Startup.wav is the sample audio file used for compression.
Comparison of performance metrics such as PSNR, MSE and compression ratio shows that Daubenches algorithm is best suited for lossless compression of speech signals. Advantages of audio compression are less storage space and associated cost, and faster data transfer.
There are several techniques for data compression. You should follow lossless compression technique as lossy audio compression results in data loss.
Image and video can be compressed in a similar way.
Steps to run the program
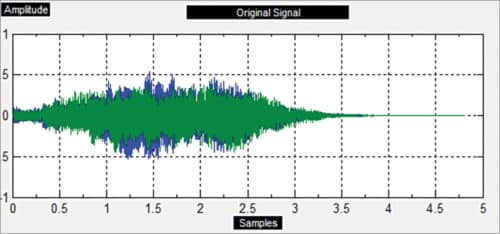
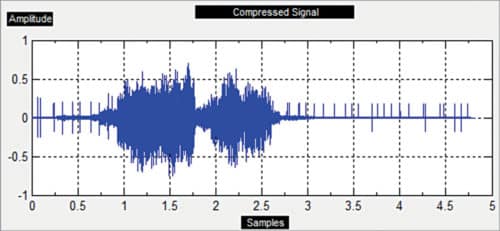
Run AudioCompresssion.m file. You will get a window as shown in Fig. 1. Select audio file and then press Compress Audio button. You will get output windows as shown in Fig. 5. Compare audio file sizes before and after compression. The compressed audio file is generated as Output1.wav in the same path as the original source file (AudioCompresssion.m).
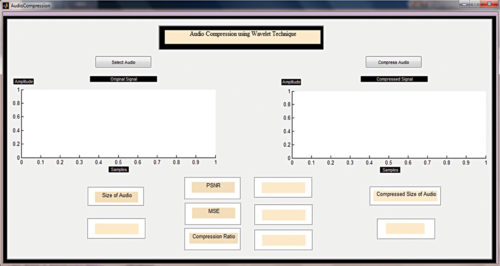
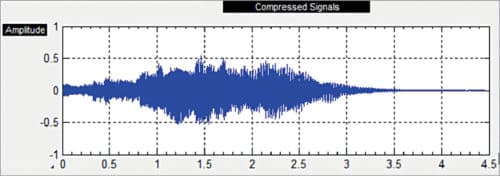
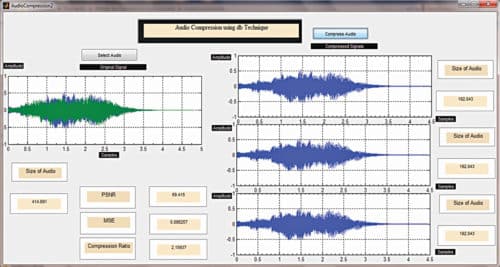
Now run AudioCompression2.m file. Select audio file and press Compress Audio button. You will get the program output window as shown in Fig. 6. Observe the size of compressed audio. Here, three compressed audio files are generated and saved in the same path as the original source file. These three outputs correspond to different discrete cosine transform (DCT) window sizes of 2, 4 and 8. The percentage change in compressed files may differ depending on the quality of original file and size.
Download Source Folder







my laptop is unable to take the audio file and in haar wavelet code select audio icon is missing
The author Lalit Patil replies: It is fully tested and it’s working fine. What may be the reason is you might have low RAM in laptop or MATLAB may be consuming higher % of CPU in laptop so GUI couldn’t load properly. You can try with good configuration of laptop.
Please sir, can I use matlab beta version for this project.
This code is showing so many errors in it what should i do??
Kindly elaborate with errors in the source code.
when running it is not showing gui…varagin function is giving errors
nyc
i cant give the input wave to 2nd method
when selecting the image i am getting error sir. i am not able to view the image.
Kindly elaborate your query.
can u please share the correct code ,im getting many errors
Kindly share the error logs.
Can u please explain what the green and blue part in the input audio waveform represent respectively?
Transient peaks along with average input signals
How do I get access to the MATLB files to run the program?
Hi, we have updated the article. The Source Folder is present at end of the article.
The problem is with the GUI, it’s not working.
It is fully tested and it’s working fine. The reason could be low RAM in your system, you may try it in another system with good configuration.
After selecting the audio in the GUI the program gives the following error.
=> Error using audioread. Too many arguments.
=>Error in gui_mainfcn – feval(varargin{:});
=>Error in gui_mainfcn(gui_State,varargin{:});
=>Error while evaluating UIControl Callback
Please check the correct code with the original code. This project was tested using Matlab R2014a. Note that there are some compatibility issues in Matlab version, you can also check them in your Matlab environment.
Good day sir, can a Pentium Silver laptop run a GUI like this? And is there a required RAM to run this GUI on Matlab sir? Thank you sir and God bless you
You have not mentioned the exact configuration of your Laptop but if you have 4GB RAM and 10GB HD, you can run MATLAB 2014a. Note that there are advantages having higher RAM and HD memories for running tool like Matlab.
The GUI is not showing any result.
The steps to run the code are given in the Source Code folder. Please go through the steps and try again using MATLAB 2014a or similar version.
i got input when i pressed compress icon..its shows following error
Error using wavread (line 70)
Invalid Wave File. Reason: Cannot open file.
Error in AudioCompression>pushbutton2_Callback (line 106)
[x,Fs,bits] = wavread(file_name);
Error in gui_mainfcn (line 95)
feval(varargin{:});
Error in AudioCompression (line 42)
gui_mainfcn(gui_State, varargin{:});
Error in
@(hObject,eventdata)AudioCompression(‘pushbutton2_Callback’,hObject,eventdata,guidata(hObject))
Error while evaluating uicontrol Callback
Thats probabyl because your using newer version of Matlab, because wavread and wavwrite works on Matlab 2014 and older. So replace it with audioread and audiowrite, also erase the bits
Can you please share your e-mail? I have multiple query and I wanted to share many photos of the program as it is having some issues.
Thank You!
Yes sure, our email id is [email protected]
sir, i am getting this error
Too many outputs requested. Most likely cause is missing [] around left hand side that has a comma separated list expansion.
Error in AudioCompression2>pushbutton2_Callback (line 85)
SIZE = fileinfo.bytes;
Error in gui_mainfcn (line 95)
feval(varargin{:});
Error in AudioCompression2 (line 42)
gui_mainfcn(gui_State, varargin{:});
Error in @(hObject,eventdata)AudioCompression2(‘pushbutton2_Callback’,hObject,eventdata,guidata(hObject))
Error while evaluating UIControl Callback
please help me ..