Read Part 1
Unbundle-by-Name function. It returns the cluster elements whose names you specify as shown in Fig. 6. Input cluster is the cluster whose elements you want to access and element 0..m-1 is the element of input cluster called 0..m-1.

We do not have to keep track of the order of the elements within the cluster. This function does not require the number of elements to match the number in the cluster. After you wire a cluster to this function, you can select individual elements from the function.
Logarithm Base 2 function. It computes base 2 logarithm of x. If x is 0, log2(x) is negative infinity as shown in Fig. 7. Here, x can be a scalar number, array or cluster of numbers, array of clusters of numbers and so on. log2(x) is of the same numeric representation as x.
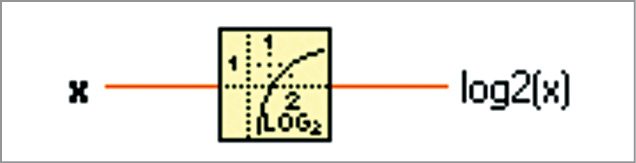
Bundle function. If x is not complex and is less than 0, log2(x) is NaN (not a number).
It assembles a cluster from individual elements as shown in Fig. 8. The cluster is one whose value you want to change and element 0..n-1 accepts any data type, and output cluster is the resulting cluster.
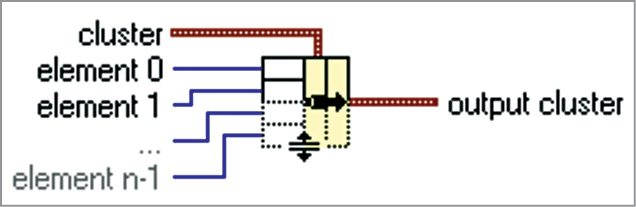
You can also use this function to change the values of individual elements in an existing cluster without having to specify new values for all elements. To do so, wire the cluster you want to change to the middle cluster terminal of this function. When you wire a cluster to this function, function resizes automatically to display inputs for each element in the cluster.
Quotient and Remainder function. Computes integer quotient and remainder of the two inputs as shown in Fig. 9. x and y can be scalar numbers; x-y*floor(x/y) is the remainder and floor(x/y) is the integer quotient. This function rounds floor(x/y) to the nearest integer towards infinity.

Clusters. Clusters group data elements of mixed types as shown in Fig. 10. A cluster is similar to a record or struct in text based programming languages. An example of a cluster is LabVIEW error cluster, which combines a Boolean value, a numeric value and a string.
Bundling several data elements into clusters eliminates wire clutter on the block diagram and reduces the number of connector pane terminals that subVIs need. The connector pane has, at most, 28 terminals. If your front panel contains more than 28 controls and indicators that you want to pass to another VI, group some of these into a cluster and assign the same to a terminal on the connector pane.

Most clusters on the block diagram have a pink wire pattern and data-type terminal. Error clusters have a dark-yellow wire pattern and data-type terminal. Cluster elements have a logical order unrelated to their position in the shell. The first object you place in the cluster is element 0, second is element 1 and so on. If you delete an element, the order adjusts automatically. The cluster order determines the order in which the elements appear as terminals on Bundle and Unbundle functions on the block diagram.
Download Source Code: click here
K.M. Abubeker, Jose J. Edathala and Shinto Sebastian are assistant professors in the department of electronics and communications engineering, Amal Jyothi College of Engineering, Kottaym, Kerala







